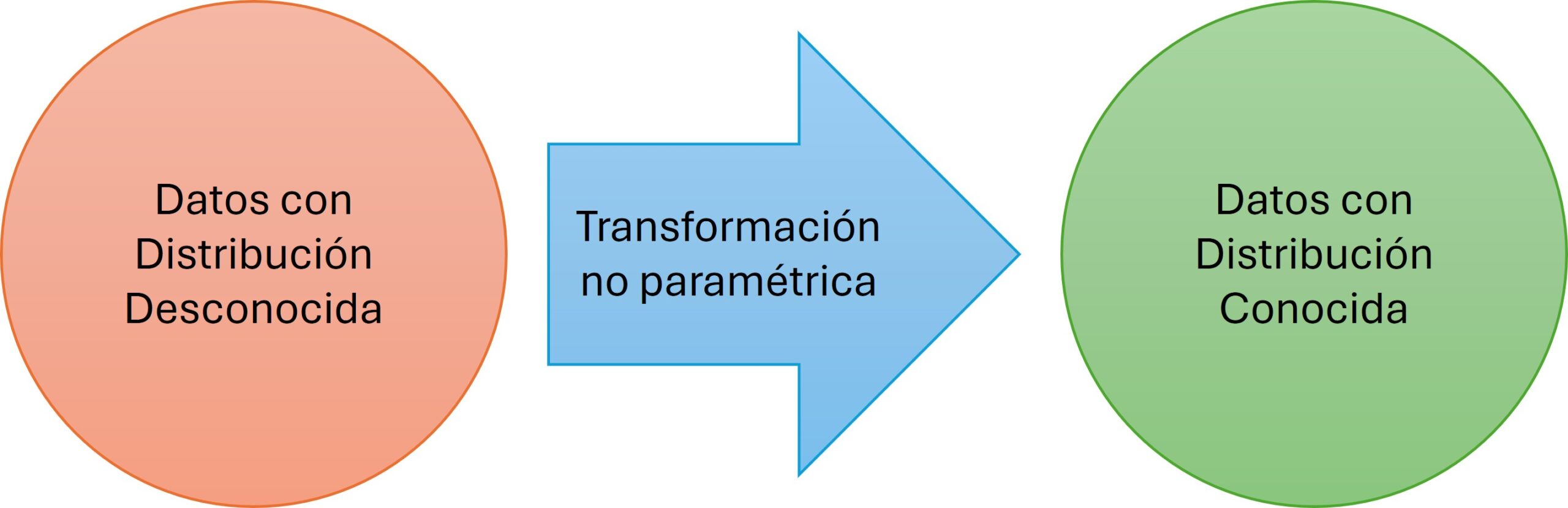
Puntajes Normales Secuenciales: una herramienta moderna para el monitoreo estadístico de procesos

Los puntajes normales secuenciales, también conocidos como sequential normal scores, son una transformación no paramétrica que permite extender el uso de métodos paramétricos de monitoreo estadístico para su uso no paramétrico. Es decir, cuando tus datos no siguen una distribución normal o alguna otra requerida. Transformaciones paramétricas tradicionales pueden generar errores de modelación que logras mitigar al moverte a un enfoque no paramétrico.

En el mundo de la ingeniería industrial y de la calidad, uno de los retos más frecuentes es monitorear procesos en tiempo real. Esto implica analizar secuencias de datos que llegan de manera continua, como la vibración de un rodamiento, el tiempo de servicio de un cajero o la temperatura de un horno.

La mayoría de los métodos clásicos de control estadístico de procesos (como las gráficas de control Shewhart, CUSUM o EWMA) fueron diseñados bajo un supuesto fuerte: que los datos son independientes y provienen de una distribución normal. Pero, ¿qué pasa cuando los datos no cumplen esta condición?

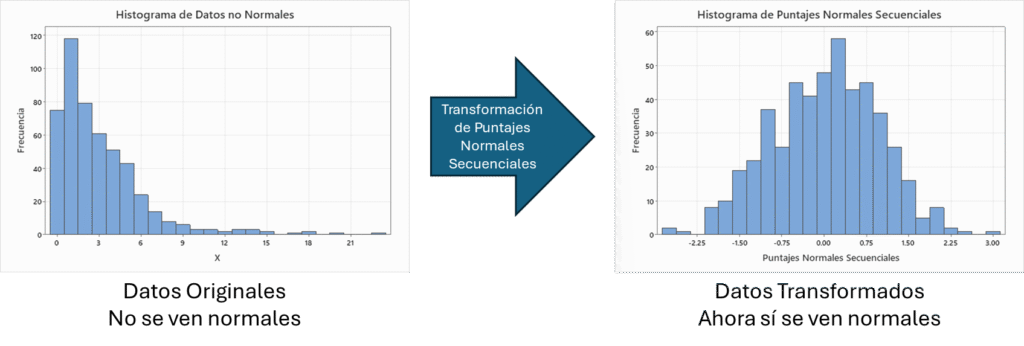
Existen muchas formas de responder esta pregunta. Una estrategia moderna y poderosa para resolver este problema es utilizando puntajes normales secuenciales. Los puntajes normales secuenciales son una transformación no paramétrica diseñada para el monitoreo de datos que normaliza tus observaciones. Tal como se ilustra en la Figura 1, esto permite extender el uso de métodos tradicionales de monitoreo a situaciones donde tus datos ya no cumplen el supuesto de normalidad.

Los puntajes normales secuenciales transforman tus datos para que sigan una distribución normal estándar. — Figura 1. La transformación de puntajes normales secuenciales permite que cualquier serie independiente de datos se aproxime a la distribución normal.

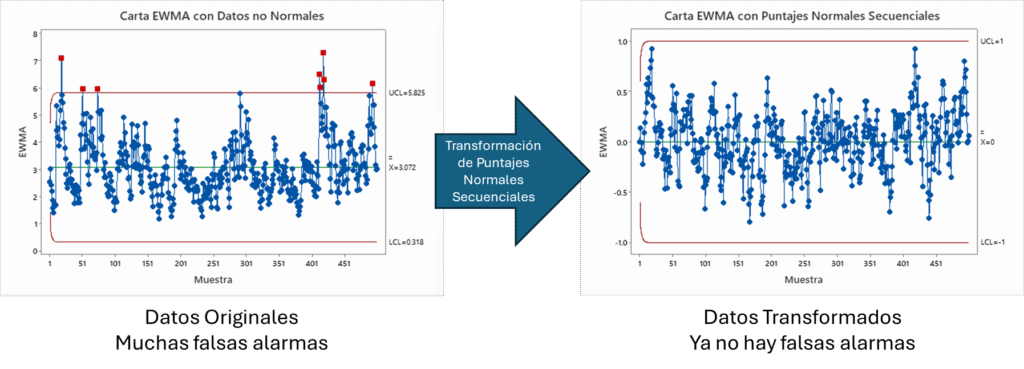
Imagina poder utilizar una carta Shewhart, EWMA o CUSUM cuando tus observaciones bajo control no son normales. Esta es una situación común en servicios con sus mediciones de tiempos de ciclo, procesos de manufactura con algún límite físico como la dureza, o el espesor, o en procesos modernos de IoT con sus señales de vibraciones y temperaturas. Observa en la Figura 2 como gracias a los puntajes normales secuenciales es posible utilizar una gráfica EWMA con un mejor control de las falsas alarmas.

Los puntajes normales secuenciales te permiten utilizar herramientas paramétricas que asumen normalidad aunque los datos originales no siguan este comportamiento. — Figura 2. Carta EWMA con datos nor normales y con los mismos datos transformados con puntajes normales secuenciales.

Usando transformaciones paramétricas tracicionales como la transformación Box-Cox o la transformación de Johnson corres el riesgo de cometer errores de modelación. Como se discute en este artículo sobre la importancia de la normalidad en el monitoreo estadístico, las transformaciones paramétricas pueden ser peligrosas. Como alternativa, las transformaciones no paramétricas como la transformación de puntajes normales tienden a ser más seguras bajo condiciones muy generales.

A través de esta página analizaremos el problema de los datos no normales, cómo funcionan los enfoques no paramétricos, y cómo se desarrolla la alternativa de los puntajes normales secuenciales como estrategia no paramétrica para el monitoreo y/o control estadístico. Al final del documento encontrarás tips avanzados para resolver estas transformaciones utilizando un paquete de disponible en lenguaje R llamado SNSchart.

El problema: datos no normales y los enfoques no paramétricos tradicionales

Cuando los datos no son normales —por ejemplo, presentan asimetría, colas pesadas o valores atípicos—, los métodos paramétricos pierden potencia para detectar cambios.

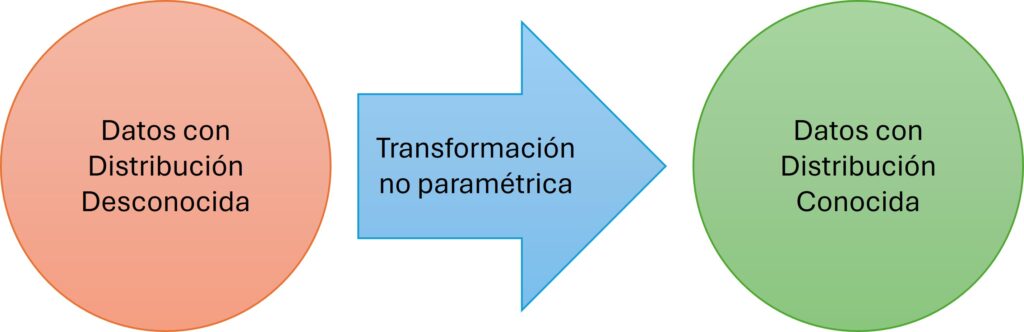
Una alternativa muy utilizada son los métodos no paramétricos. Estos, en lugar de trabajar con los valores originales, típicamente usan transformaciones ingeniosas cuyo resultado puede ser caracterizado de forma exacta, aunque la distribución original de los datos sea desconocida. En la Figura 3 se ilustra este enfoque de transformaciones no paramétricas.

La mayor parte de las transformaciones no paramétricas se basan en el análisis de la posición relativa de los datos, y para ello no se requiere conocer la distribuión original. — Figura 3. Una transformación no paramétrica apropiada puede ayudarte a analizar tus datos cuando no tienes un marco de referencia, o distribución, conocida.

Probablemente la transformación más utilizada sea la transformación de rangos. La transformación de rangos es la base de la mayor parte de los métodos no paramétricos populares. Como se ejemplifica en la Tabla 1. La idea es sencilla: en lugar de preocuparse por la forma de la distribución de los datos, basta con conocer el orden relativo en que se encuentran las observaciones.

i:	1	2	3	4	5	6	7
x:	3.0	4.5	8.6	2.3	2.8	1.7	6.6
r:	4	5	7	2	3	1	6

Tabla 1. La transformación de rangos cambia el valor de tus datos (x) por su posición relativa en el grupo (r).

Observa en la tabla que la observación más pequeña, x =1.7, en la sexta posición i = 7, recibe el rango de r = 1. La segunda más pequeña, 2.3, recibe el rango de 2, y así hasta la observación más grande, 8.7, que recibe el rango más alto que es 7. La letra i corresponde al orden o posición en que las mediciones fueron tomadas.

El inconveniente es que, en un contexto secuencial, volver a calcular todos los rangos cada vez que llega un nuevo dato es computacionalmente costoso, especialmente si hablamos de grandes volúmenes de información. Un contexto secuencial típico es, por ejemplo, un proceso de manufactura, donde las mediciones aparecen según el orden de la producción.

La solución: rangos secuenciales

Para enfrentar este reto, Parent (1965) propuso los rangos secuenciales:

Cuando llega un nuevo dato, solo se calcula su rango relativo a los datos anteriores.
Los rangos previos permanecen intactos.

En la Tabla 2 se muestra que los rangos se calculan ahora sólo utilizando la información previa de la secuencia observada.

i:	1	2	3	4	5	6	7
x:	3.0	4.5	8.6	2.3	2.8	1.7	6.6
r:	1	2	3	1	2	1	6

Tabla 2. La transformación de rangos secuenciales cambia el valor de tus datos (x) por su posición relativa (r) en relación a lo previamente observado en la secuencia (i).

Por ejemplo, la primera observación medida recibe el rango 1, pues no hay observaciones anteriores, así que 1 es el único rango posible para asignar. La segunda observación, 4.5, recibe el rango de 2, pues es la mayor de dos observaciones hasta ese momento . La tercera observación 8.6, recibe el rango de 3, pues es la mayor de las tres que van. Y así, la cuarta observación 2.3 recibe nuevamente el rango 1, por ser la menor de entre sus predecesoras.

Si encontramos empates en nuestras observaciones, utilizamos el rango promedio. Por ejemplo, en una secuencia de observaciones 2, 4, 7, 3, 4 sería ranqueada como 1, 2, 3,2, 3.5. Observa que la quinta observacion, que es 4, está empatada con la primera, que también es 4. Si la segunda observación fuese menor, la quinta observación tendría un rango de 4, si fuese mayor, la quinta tendría un rango de 3. Cualquier fracción entre 3 y 4 estaría correcta, así que optamos por tomar el promedio entre los posibles rangos, esto es, 3.5.

Los rangos se asignan según lo observado hasta el momento, y estos no cambian aún cuando aparecen nuevas observaciones. Esto ahorra muchísimo tiempo de cómputo. Sin embargo, hay un problema: las distribuciones resultantes son difíciles de caracterizar teóricamente, lo que limitaba su aplicación práctica.

Un paso más: los puntajes normales secuenciales

Aquí es donde surge la propuesta de puntajes normales secuenciales (o simplemente SNS por sequential normal scores). La idea es transformar cada rango secuencial en el cuantil equivalente de una distribución normal estándar.

Dicho de otra forma:

Tomamos el rango secuencial del nuevo dato.
Lo transformamos a una probabilidad acumulada dentro del intervalo (0,1).
Esa probabilidad se traduce en el valor correspondiente de la curva normal estándar N(0,1).

El resultado es una secuencia de valores que:

Son independientes entre sí (una gran ventaja frente a los rangos tradicionales).
Se comportan asintóticamente como una distribución normal estándar.

Para transformar los rangos secuenciales a una probabilidad acumulada $p$ lo único que tenemos que hacer es restar el valor de 0.5 al rango secuencial y dividir entre el número de observaciones utilizadas al momento de calcular los rangos. A la cantidad de observaciones utilizadas en un ranqueo le llamamos orden del rango, o simplemente $O$ . Así, la fórmula para el paso 2 es

$\begin{align*} p = \frac{r-0.5}{O}. \end{align*}$

El valor de 0.5 es una corrección útil para balancear las probabilidades calculadas y evitar imposibilidades cuando convertimos estas probabilidades en valores $z$ .

Para el paso 3, necesitamos obtener el valor $z$ de una normal estándar que genera esta probabilidad acumulada. Esto lo podemos obtener de tablas de valores z para la normal estándar, o evaluando funciones en Excel como NORM.S.INV(), o qnorm() en R.

De manera general, con lenguaje un poco más técnico, se dice que el valor $z$ se obtiene evaluando la probabilidad acumulada $p$ en la inversa de una función de distribución acumulada normal estándar

$\begin{align*} z = \Phi^{-1}(p). \end{align*}$

El símbolo $\Phi$ es utilizado en estadística para representar a la distribución normal estándar acumulada. Y el -1 en la función no representa el recíproco, sino que indica que se trata de la función inversa.

Haciéndo un paréntesis matemático, se puede decir que la inversa es cómo el resultado de hacer un despeje. Si la función es   , entonces la función inversa es . En la primera la entrada es  y el resultado es , en la inversa la entrada es  y la salida es . Así, la función de distribución acumulada de una normal estándar tiene como entrada un valor de  y esta te arroja una probabilidad acumulada , y la inversa tienen como entrada la probabilidad acumulada  y genera como resultados un valor de . Se utiliza el concepto de inversa pues de la distribución normal acumulada no se puede despejar del valor de  para ponerlo en términos de . Se tienen que utilizar métodos numéricos para esto, o evaluar tablas con valores pre-calculados.

Siguiendo con el ejemplo mostrado en la Tabla 2, podemos calcular los puntajes normales secuenciales obteniendo las probabilides acumuladas y evaluando las mismas en la inversa de una normal estándar. Tal como se muestra en la Tabla 3.

i:	1	2	3	4	5	6	7
x:	3.0	4.5	8.6	2.3	2.8	1.7	6.6
r:	1	2	3	1	2	1	6
p:	0.5	0.75	0.83	0.13	0.30	0.08	0.79
z:	0.00	0.67	0.97	-1.15	-0.52	-1.38	0.79

Tabla 3. Primero se calculan los rangos secuenciales (r), luego la probabilidad acumulada (p), y finalmente el puntaje normal (z).

Observa que la primer observación, 3.0, tiene un rango secuencial de 1, cuya probabilidad acumulada se estima como (1-0.5) / 1 = 0.5. Puesto que el valor $z$ de una normal estándar que genera una probabilidad acumulada es cero, entonces el valor 3.0 se queda transformado en 0. El proceso se repite en cada una de las observaciones.

¿Por qué es útil esta transformación?

La gran ventaja de los puntajes normales secuenciales es que extienden el uso de los métodos paramétricos a situaciones donde los datos no son normales.

En otras palabras: aunque los datos originales sean asimétricos o provengan de una distribución desconocida, los puntajes normales secuenciales permiten ser tratados como si fueran normales e independientes con media 0 y desviación estándar de 1. Esto significa que se pueden aplicar directamente sobre ellos herramientas clásicas como:

Gráficas Shewhart
Gráficas CUSUM.
Gráficas EWMA.
Procedimientos secuenciales para detectar cambios en la media o en la variabilidad.

El único cuidado que hay que tener es con enfoques tipo Shewhart, donde el monitoreo de observaciones individuales requiere de al menos 370 observaciones previas bajo control para detectar un cambio al usar límites de 3 sigmas. Este número se reduce rápidamente a 29 con subgrupos tamaño 2 y a 5 para subgrupos tamaño 5. Enfoques tipo CUSUM y EWMA requieren muy pocas observaciones iniciales para detectar cambios en el proceso.

Ejemplo ilustrativo

Para illustrar la aplicación de esta novedosa transformación. Utilizamos datos obtenidos de Tercero-Gomez, V., Ramirez-Galindo, J., Cordero-Franco, A., Smith, M., & Beruvides, M. (2012). Estos datos mostrados en la Tabla 4 corresponden a una secuencia que se lee de izquierda a derecha y de arriba hacia abajo. Es decir, 15.18 es la primera observación, seguida de 7.82, y así sucesivamente.

Estos datos provienen de tiempos medidos en segundos entre llegadas a la biblioteca de Texas Tech University. Son 100 observaciones. De estas, a las últimas 20 de la serie se les aplicó una reducción de 3 segundos para simular un cambio de comportamiento.

15.18	7.82	3.6	24.32	6.3	61.94	17.55	10.32	7.12	20
6.64	46.18	11.13	9.46	4.2	12.78	14.63	41.44	17.1	13.38
4.84	17.1	44.28	53.89	13.41	27.6	12.6	6.88	16.35	8.49
5.34	6.25	19.79	8.51	5.08	13.81	11.22	10.47	62.56	4.11
19.95	3.07	14.1	41.16	3.11	7.75	3.48	18.82	18.17	3.79
4.71	40.28	6.99	4.29	7.14	28.68	26.33	10.14	48.08	12.72
7.44	14.26	16.75	50.29	12.65	37.37	3.32	21.7	18.25	4.17
17.22	3.59	17.03	9.52	18.06	4.25	8.55	10.49	2.9	4.91
6.52	38.14	5.61	2.61	4.47	21.63	1.43	16.56	10.94	3.18
6.84	2.02	0.8	6.5	15.25	5.87	9.04	8.32	1.24	0.84

Tabla 4. Tiempo entre llegadas a la biblioteca universitaria en Texas Tech University.

Las observaciones están lejos de ser normales, como es lo esperado en la medición de tiempos de ciclo. Para analizarlas aplicamos la transformación de puntajes normales secuenciales. El resultado de esta transformación aparece en la Tabla 5 a continuación.

0.00	-0.67	-0.97	1.15	-0.52	1.38	0.37	-0.16	-0.59	0.67
-0.75	1.15	0.00	-0.27	-1.28	0.24	0.30	1.09	0.41	0.06
-1.18	0.41	1.23	1.53	0.00	0.80	-0.28	-0.85	0.26	-0.57
-1.21	-1.08	0.65	-0.42	-1.28	0.17	-0.14	-0.23	2.23	-1.78
0.73	-2.26	0.24	1.05	-1.83	-0.54	-1.61	0.64	0.60	-1.34
-1.05	1.06	-0.55	-1.09	-0.42	1.03	0.90	-0.20	1.56	0.02
-0.47	0.27	0.41	1.60	-0.04	1.00	-1.78	0.75	0.53	-1.24
0.44	-1.53	0.35	-0.29	0.52	-1.09	-0.33	-0.15	-2.49	-0.86
-0.66	1.14	-0.76	-2.51	-0.95	0.83	-2.53	0.36	-0.06	-1.55
-0.52	-2.14	-2.55	-0.55	0.38	-0.63	-0.16	-0.25	-2.17	-2.17

Tabla 5. Puntajes normales secuenciales correspondientes al ejemplo de tiempos entre llegadas de la Tabla 4.

Cuando las mediciones están en control, los puntajes normales secuenciales se aproximan a una distribución normal estándar con media 0 y desviación estándar 1. Así, para hacer un monitoreo con un EWMA diseñado para distribuciones normales, sólo tenemos que considerar que la media y desviación estándar son los valores conocidos 0 y 1, correspondientemente.

La aplicación de este EWMA sobre los puntajes normales lo podemos ver en la Figura 4.

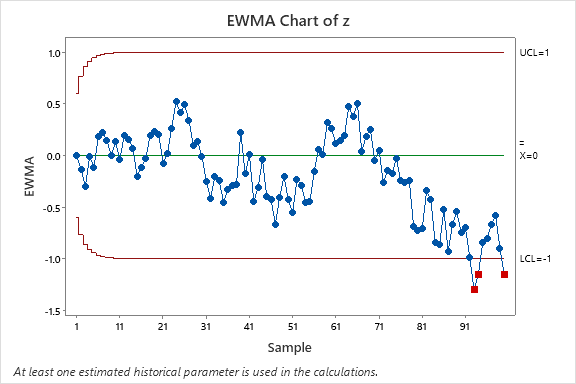
Aplicamos un EWMA que asume normalidad sobre los puntajes normales secuenciales para su análisis. — Figura 4. EWMA tradicional con $\lambda = 0.2$ aplicado sobre los puntajes normales secuenciales.

Observamos en la Figura 4 que efectivamente se detectó un cambio en la tendencia media al final de la secuencia, que es justo donde creamos un cambio.

Algunas Consideraciones

Los puntajes normales secuenciales ofrecen muchas ventajas, pues permiten ampliar la aplicación de herramientas paramétricas, que asumen normalidad e independencia de las mediciones, para ser usadas como herramientas no paramétricas en situciones donde los datos no siguen una distribución específica. Sin embargo, hay que tomar algunas precauciones.

Si conoces la distribución de tus datos, es mejor usar el método paramétrico correspondiente. Así podrás detectar mejor los cambios.
Utiliza observaciones históricas en las que confíes. Los rangos secuenciales se calculan ranqueando la observación actual en relación a observaciones anteriores. Si piensas que algunas observaciones anteriores no estaban en control, quítalas, y ranquea utilizando sólo aquellas en las que sí confías.
Cartas tipo EWMA y CUSUM son apropiadas para se usadas con puntajes normales secuenciales. Pocos datos iniciales son suficientes para detectar cambios. Estas cartas son recomendadas cuando tienes observaciones individuales.
Cartas tipo Shewhart requieren de muchos datos iniciales para detectar rápidamente un cambio en el proceso. Estas cartas son apropiadas cuando tienes observaciones en forma de subgrupos, donde la necesidad de muchos datos es menor.

Software

Puedes utilizar el paquete de R SNSchart como una herramienta para transformar tus datos en puntajes normales secuenciales . Específicamente la función SNS() te será útil para transformar tus datos. Para ilustrar el uso del software, vemos un caso de la industria de servicio bancario de Taiwan.

Los archivos que utilizaremos para este ejemplo son ICbank.csv y BankNew.csv. El primero se puestra en la Tabla 6 y el segundo en la Tabla 7. La Tabla 6 tiene datos de referencia en control, y la Tabla 7 muestra las observaciones que se desean evaluar.

Como vemos en la Tabla 6, se midieron tiempos de servicio, en minutos, en 10 ventanillas, cada 2 días durante 30 días. Esto es, se obtuvieron 15 muestras de 10 observaciones cada una. La Tabla 7 contiene 10 muestras con los nuevos tiempos de servicio.

i	X₁	X₂	X₃	X₄	X₅	X₆	X₇	X₈	X₉	X₁₀
1	0.88	0.78	5.06	5.45	2.93	6.11	11.59	1.20	0.89	3.21
2	3.82	13.40	5.16	3.20	32.27	3.68	3.14	1.58	2.72	7.71
3	1.40	3.89	10.88	30.85	0.54	8.40	5.10	2.63	9.17	3.94
4	16.80	8.77	8.36	3.55	7.76	1.81	1.11	5.91	8.26	7.19
5	0.24	9.57	0.66	1.15	2.34	0.57	8.94	5.54	11.69	6.58
6	4.21	8.73	11.44	2.89	19.49	1.20	8.01	6.19	7.48	0.07
7	15.08	7.43	4.31	6.14	10.37	2.33	1.97	1.08	4.27	14.08
8	13.89	0.30	3.21	11.32	9.90	4.39	10.50	1.70	10.74	1.46
9	0.03	12.76	2.41	7.41	1.67	3.70	4.31	2.45	3.57	3.33
10	12.89	17.96	2.78	3.21	1.12	1.26	4.23	6.18	2.33	6.92
11	7.71	1.05	1.11	0.22	3.53	0.81	0.41	3.73	0.08	2.55
12	5.81	6.29	3.46	2.66	4.02	10.95	1.59	5.58	0.55	4.10
13	2.89	1.61	1.30	2.58	18.65	10.77	18.23	3.13	3.38	6.34
14	1.36	1.92	0.12	11.08	8.85	3.99	4.32	1.71	1.77	1.94
15	21.52	0.63	8.54	3.37	6.94	3.44	3.37	6.37	1.28	12.83

Tabla 6. Muestra en control de tiempos de servicio en minutos en 10 ventanillas bancarias, cada 2 días durante 30 días.

i	X₁	X₂	X₃	X₄	X₅	X₆	X₇	X₈	X₉	X₁₀
16	3.54	0.01	1.33	7.27	5.52	0.09	1.84	1.04	2.91	0.63
17	0.86	1.61	1.15	0.96	0.54	3.05	4.11	0.63	2.37	0.05
18	1.45	0.19	4.18	0.18	0.02	0.70	0.80	0.97	3.60	2.94
19	1.37	0.14	1.54	1.58	0.45	0.61	0.74	1.74	3.92	4.82
20	3.80	2.46	0.06	1.80	3.25	2.13	2.22	1.37	2.13	0.25
21	1.59	3.88	0.39	0.54	1.58	1.70	0.48	1.25	6.83	0.31
22	5.01	1.85	3.10	1.00	0.09	1.16	2.69	2.79	1.84	0.62
23	4.96	0.55	1.43	4.12	4.06	1.42	1.43	0.86	0.67	0.13
24	1.08	0.65	0.91	0.82	2.88	1.76	2.87	1.97	0.62	1.76
25	4.56	0.44	5.61	2.79	1.73	2.46	0.53	1.73	7.02	2.13

Tabla 7. Muestras a evaluar de tiempos de servicio en minutos en 10 ventanillas bancarias.

Cargamos el paquete SNSchart instalándolo y leyendo la librería correspondiente.

install.packages("SNSchart") #este paso se puede omitir si ya está instalado
library(SNSchart)

Luego procedemos a leer los datos de los archivos con las mediciones en control que usaremos como referencia y las mediciones que deseamos evaluar.

phaseI = read.csv("ICbank.csv") # mediciones en control
phaseII = read.csv("BankNew.csv") # mediciones a evaluar

Para hacer el análisis requerimos preparar tres vectores: (1) datos en control, (2) datos a evaluar, y (3) índice de subgrupos.

# Vector Y: Datos en control de Fase 1
X <- phaseII[c("x1","x2","x3","x4","x5","x6","x7","x8","x9","x10")]
Y <- phaseI[c("x1","x2","x3","x4","x5","x6","x7","x8","x9","x10")]
Y <- stack(Y)$values

# Vector X: Datos a evaluar
data = t(X)
data = as.data.frame(data)
data = stack(data)
X = data$values

# Vector X.id: Índice que indica a qué subgrupo pertenece cada dato a evaluar
X.id = as.numeric(data$ind)

Ya que tenemos estos tres vectores numéricos, procedemos a evaluarlos con la función SNS() y a guardar los resultados de este análisis en la variable s.

s = SNS(
  X = X, # vector numérico con los datos a evaluar.
  X.id = X.id, # índice numérico indica subgrupo de cada valor de X.
  Y = Y, # vector numérico con los datos de fase I. Es opcional.
  chart = "Shewhart", # carta de control a utilizar.
  chart.par = c(3), # parámetro de la carta de control definida.
  snsRaw = TRUE, # TRUE si queremos recuperar los datos transformados.
  isFixed = FALSE, # FALSE para tomar en cuenta las nuevas mediciones X.
  omit.id = NULL, # Si queremos que algunas obs. no se tomen en cuenta.
  auto.omit.alarm = FALSE # FALSE toma en cuenta datos con señal de alarma.
)

Si todo salió bien puedes pedirle a R que dibuje una carta de control Shewhart con los puntajes normales obtenidos. Para esto ejecutamos la función plot(s). El resultado de esta gráfica se observa en la Figura 5. En la gráfica se observa el monitoreo del estadístico $Z_i = \sum_j^n z_{ij} / \sqrt(n)$ . Esto es, $Z_i$ es la suma de los puntajes normales secuenciales en un subgrupo dividida entre la raíz del número de observaciones por subgrupo. Así, $Z_i$ sigue una distribución normal estándar, y los límites de control para la carta Shewhart de 3 sigmas son -3 y 3, tal como se observa en la figura.

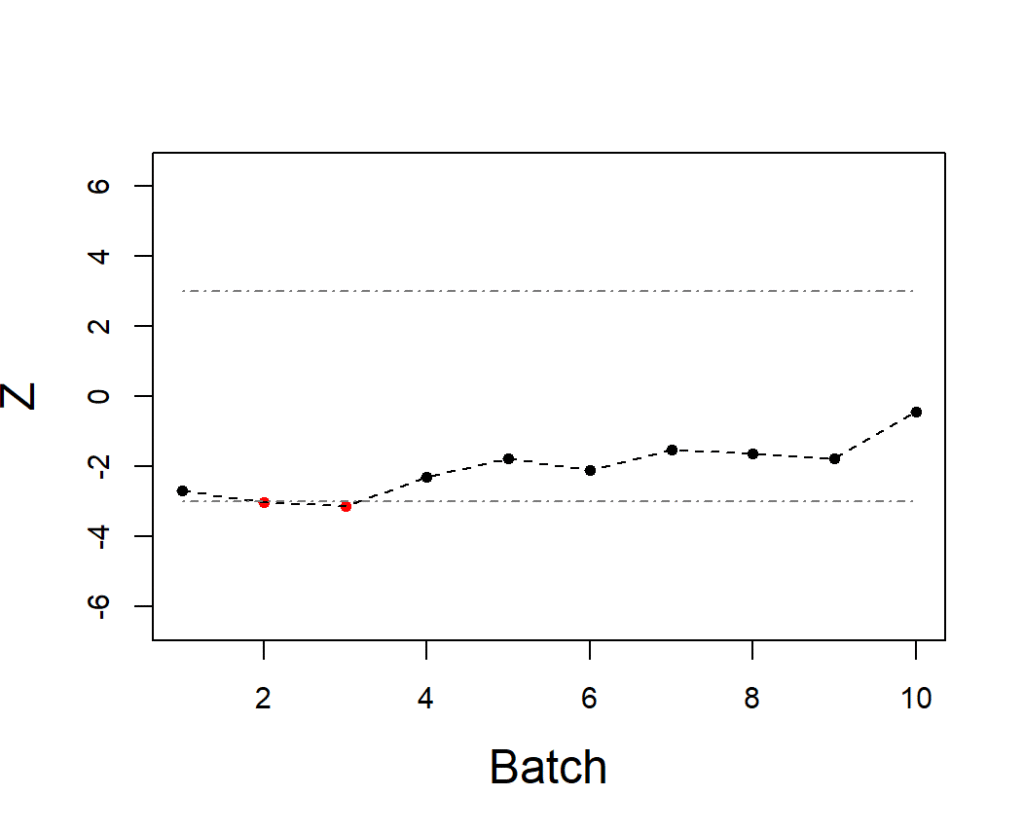
Los puntajes normales secuenciales mostraron un cambio enla media de los datos al ser analizados con una carta Shewhart para medias. — Figura 5. Carta de control Shewhart para puntajes normales obtenida del paquete SNSchart de R.

Si sólo queremos los datos transformados para analizarlos con el software de preferencia, estos los podemos obtener ejecutando s$Zraw. Esto mostrará un vector con los datos transformados que he tabulado en la Tabla 8.

i	z₁	z₂	z₃	z₄	z₅	z₆	z₇	z₈	z₉	z₁₀
1.000	-0.100	-2.715	-0.883	0.540	0.269	-1.992	-0.638	-1.196	-0.338	-1.409
2.000	-1.201	-0.699	-0.963	-1.139	-1.488	-0.268	0.125	-1.340	-0.468	-2.156
3.000	-0.698	-1.708	0.192	-1.708	-2.375	-1.205	-1.176	-1.040	0.044	-0.207
4.000	-0.653	-1.675	-0.602	-0.594	-1.404	-1.269	-1.127	-0.490	0.167	0.353
5.000	0.171	-0.252	-1.985	-0.404	-0.013	-0.334	-0.334	-0.622	-0.334	-1.471
6.000	-0.514	0.239	-1.391	-1.299	-0.536	-0.458	-1.328	-0.718	0.702	-1.391
7.000	0.481	-0.314	-0.012	-0.854	-1.775	-0.724	-0.107	-0.083	-0.320	-1.125
8.000	0.509	-1.187	-0.548	0.396	0.371	-0.548	-0.548	-0.929	-1.030	-1.669
9.000	-0.770	-1.039	-0.852	-0.917	-0.022	-0.320	-0.022	-0.224	-1.107	-0.320
10.000	0.558	-1.346	0.684	0.005	-0.317	-0.078	-1.296	-0.317	0.867	-0.167

Tabla 8. Puntajes normales secuenciales obtenidos de la transformación aplicada sobre las observaciones de la Tabla 7.

Hay que hacer notar que al trabajar con subgrupos, las observaciones de cada subgrupo se ranquean utilizando observaciones anteriores junto a la observación ranqueada. Las observaciones dentro del mismo subgrupo no se ranquean entre sí. Esto facilita que cuando haya un subgrupo fuera de control, el cambio en este subgrupo se note más, al tiempo que la independencia entre las observaciones dentro del mismo subgrupo se mantiene.

Las aplicaciones de los puntajes normales secuenciales son amplias, y muchas de estas aplicaciones las puedes encontrar automatizadas en el paquete SNSchart. Puedes explorar esta y otras aplicaciones en esta liga.

Conclusión

Los puntajes normales secuenciales representan un puente entre el mundo paramétrico y el no paramétrico. Gracias a esta transformación:

Podemos analizar datos no normales con las herramientas de siempre.
Se reducen los costos computacionales al no recalcular rangos completos.
Se habilita el monitoreo eficiente de grandes flujos de datos en tiempo real, algo cada vez más común en la era de la Industria 4.0.

Así, los puntajes normales secuenciales son una estrategia moderna y poderosa para practicantes de la administración cuatitativa de procesos e ingenieros que buscan monitorear procesos industriales con mayor robustez y flexibilidad.