Una función elemental del ingeniero de calidad es la medición la capacidad de procesos. Esto es, una medición de lo que el proceso puede dar bajo ciertas condiciones. Su conocimiento es fundamental para establecer planes de producción, contratos con clientes, acuerdos con proveedores, y es un indicador útil para guiar los esfuerzos de mejora. Sin embargo, no es inusual encontrar empresas, algunas de clase mundial, donde los reportes de capacidad no corresponden realmente a una medición de capacidad.
En este artículo discuto brevemente el concepto de capacidad, desde su origen histórico hasta sus usos modernos. Prestamos especial atención a las condiciones necesarias para una correcta medición de capacidad. Continuamos con la discusión de algunas mediciones tradicionales para observaciones variables como lo son el ![]() o el
o el ![]() , y cerramos con algunas alternativas útiles para medir la capacidad en procesos cuyas mediciones son cualitativas o de atributos.
, y cerramos con algunas alternativas útiles para medir la capacidad en procesos cuyas mediciones son cualitativas o de atributos.
El concepto de capacidad de procesos
Tras realizar una investigación sobre nuevas formas para medir la capacidad de procesos en Salazar-Alvarez, Temblador-Pérez, Conover, Tercero-Gómez, Cordero-Franco y Beruvides (2016), encontramos que el origen del concepto de capacidad junto a sus métricas es particularmente difuso. En una recapitulación de hechos, Rodriguez (1992) menciona que las técnicas para analizar la capacidad se han venido usando desde los años 80. Como ejemplo de esto vemos que Kane (1986), al introducir los índices de capacidad ![]() y
y ![]() , populares hasta el día de hoy, no duda en indicar que estos ya eran utilizados en distintas compañías de Japón y la industria automotriz de los Estados Unidos. Desde entonces han sido muchos los que abogan por el concepto de capacidad y su medición.
, populares hasta el día de hoy, no duda en indicar que estos ya eran utilizados en distintas compañías de Japón y la industria automotriz de los Estados Unidos. Desde entonces han sido muchos los que abogan por el concepto de capacidad y su medición.
Entre los promotores de este concepto encontramos a Frank M. Gryna, quien en el manual de calidad de Jurán ofrece una breve pero a la vez completa definición de este concepto:
“La capacidad de un proceso es la medida de la reproducibilidad inherente de la producción de un proceso”
Frank M. Gryna (1999, p.22.11)
En otras palabras, a lo mejor un poco más relacionadas con la jerga del ingeniero de calidad, podemos decir que la capacidad de un proceso es una medida del rendimiento que tiene un proceso, pero cuando este se encuentra en un estado de control. En un artículo anterior ya habíamos visto lo que significa estar en estado de control y la relación con ser predecible (o reproducible). Así, podemos decir que una medida de capacidad de un proceso es una medida de rendimiento, pero no todas las medidas de rendimiento son medidas de capacidad, pues no todas las medidas de rendimiento corresponden a un proceso bajo control.
Capacidad de procesos para observaciones variables
Índices de capacidad de procesos
Para lidiar con procesos cuyas mediciones son cuantitativas, independientes, normales y en estado de control, Kane (1986) propone usar
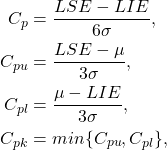
Aquí, ![]() y
y ![]() corresponden al límite superior de especificación y al límite inferior de especificación, respectivamente.
corresponden al límite superior de especificación y al límite inferior de especificación, respectivamente.
De estas medidas, el ![]() es la más importante, pues considera la falta de alineación que pueda haber entre la media del proceso y el centro de las especificaciones. El
es la más importante, pues considera la falta de alineación que pueda haber entre la media del proceso y el centro de las especificaciones. El ![]() se limita a comparar la tolerancia esperada por el cliente (numerador) con la tolerancia natural del proceso (denominador), independientemente del centrado que pueda tener el proceso. El
se limita a comparar la tolerancia esperada por el cliente (numerador) con la tolerancia natural del proceso (denominador), independientemente del centrado que pueda tener el proceso. El ![]() y el
y el ![]() son útiles para el cálculo del
son útiles para el cálculo del ![]() y ayudan a identificar si el proceso tiene un mejor desempeño cumpliendo el límite superior de especificación,
y ayudan a identificar si el proceso tiene un mejor desempeño cumpliendo el límite superior de especificación, ![]() , o el inferior,
, o el inferior, ![]() .
.
Estimaciones de la media
Como se puede observar, para el cálculo de estos índices se requiere conocer la media del proceso, ![]() , y su desviación estándar,
, y su desviación estándar, ![]() del proceso bajo control. En la práctica estos valores no se conocen y deben ser estimados. Para estimar la media usamos
del proceso bajo control. En la práctica estos valores no se conocen y deben ser estimados. Para estimar la media usamos
(1) ![]()
Esto es, el promedio de todas nuestras observaviones históricas en control que corresponden al estado actual del proceso que estamos estudiando. ![]() se refiere a las observaciones individuales, con su índice
se refiere a las observaciones individuales, con su índice ![]() correspondiente, y
correspondiente, y ![]() es el total de observaciones usadas en los cálculos. El acento ^ sobre el nombre del parámetro
es el total de observaciones usadas en los cálculos. El acento ^ sobre el nombre del parámetro ![]() es sólo una conveniencia usada en estadística para denotar que se trata de un estimador del parámetro.
es sólo una conveniencia usada en estadística para denotar que se trata de un estimador del parámetro.
Estimaciones de la desviación estándar
Para estimar la desviación estándar existen varias opciones. Si contamos con un conjunto de datos que sabemos se encuentran en control, podemos usar la desviación estándar muestral
(2) 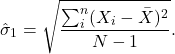
![]() es el promedio de nuestras observaciones y sigue la misma ecuación que usamos para
es el promedio de nuestras observaciones y sigue la misma ecuación que usamos para ![]() . En libros de texto de estadística encontraremos al estadístico
. En libros de texto de estadística encontraremos al estadístico ![]() con el nombre de
con el nombre de ![]() .
.
Este estimador de la desviación tiene propiedades interesantes, como que es insesgado. Es decir, en promedio, de repetir las mediciones muchas veces, este estimador nos ofrece exactamente el valor de la desviación estándar que buscamos. Sin embargo, si nuestro proceso no está bajo control, la estimación de la viabilidad puede ser mayor a la que corresponde al proceso en control.
Si no tenemos certeza que el conjunto de datos que usamos para estimar la capacidad están bajo control, entonces tenemos la opción de usar algún estimador que sea robusto a problemas en esta condición. Entre las opciones, el estimador propuesto por Shewhart para usarse en cartas de control
(3) ![]()
ha encontrado mucho eco en la práctica por ser relativamente insensible a la presencia de causas asignables de variación que afectan la media de los procesos. Esta es una condición común de falta de control, por lo que el estimador ![]() nos mitiga el efecto indeseable.
nos mitiga el efecto indeseable.
Para la estimación de ![]() requerimos de dos elementos,
requerimos de dos elementos, ![]() y
y ![]() .
. ![]() es el rango de nuestros grupo datos, es decir, la medición más grande menos la más pequeña. Si nuestros datos se encuentran divididos en subgrupos
es el rango de nuestros grupo datos, es decir, la medición más grande menos la más pequeña. Si nuestros datos se encuentran divididos en subgrupos ![]() será el promedio de los rangos calculados de cada subgrupo. Si nuestros datos están contenidos en un solo grupo,
será el promedio de los rangos calculados de cada subgrupo. Si nuestros datos están contenidos en un solo grupo, ![]() . Claro, en caso de tener un solo subgrupo, posiblemente es mejor utilizar la desviación estándar muestral. Si nuestros subgrupos de tamaño constante
. Claro, en caso de tener un solo subgrupo, posiblemente es mejor utilizar la desviación estándar muestral. Si nuestros subgrupos de tamaño constante ![]() se encuentran en el rango de 2 a 10 observaciones, podemos usar las constantes
se encuentran en el rango de 2 a 10 observaciones, podemos usar las constantes ![]() presentadas en la Tabla 1. La razón de tener valores hasta
presentadas en la Tabla 1. La razón de tener valores hasta ![]() se debe a que para valores mayores a 10 la estimación mediante el rango deja de considerarse eficiente, en términos de error, en relación a la desviación estándar muestral. Entre las alternativas para subgrupos grandes está la desviación estándar promedio, con su correspondiente corrector de sesgo, y la raíz cuadrada de la varianza ponderada. Para más detalle sobre estas últimas alternativas puedes consultar Montgomery (2020).
se debe a que para valores mayores a 10 la estimación mediante el rango deja de considerarse eficiente, en términos de error, en relación a la desviación estándar muestral. Entre las alternativas para subgrupos grandes está la desviación estándar promedio, con su correspondiente corrector de sesgo, y la raíz cuadrada de la varianza ponderada. Para más detalle sobre estas últimas alternativas puedes consultar Montgomery (2020).
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1.128 | 1.693 | 2.059 | 2.326 | 2.534 | 2.704 | 2.847 | 2.970 | 3.078 |
Índices 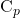 vs
vs 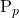
Dado que en muchas situaciones prácticas es difícil tener certeza sobre el estado de control de nuestro proceso, se prefiere estimar el ![]() y
y ![]() usando estimadores de la variación promedio dentro de los subgrupos, como es el caso del estimador basado en rangos. Cuando se usan estimadores basados en la variación global o total de todos los subgrupos, juntas las observaciones como uno solo grupo, muchos autores hacen la distinción y cambian de nombre los índices a
usando estimadores de la variación promedio dentro de los subgrupos, como es el caso del estimador basado en rangos. Cuando se usan estimadores basados en la variación global o total de todos los subgrupos, juntas las observaciones como uno solo grupo, muchos autores hacen la distinción y cambian de nombre los índices a ![]() y
y ![]() , correspondientemente. Por ejemplo, este es el caso de Minitab, donde el
, correspondientemente. Por ejemplo, este es el caso de Minitab, donde el ![]() y el
y el ![]() estarían representando la capacidad global del proceso. Sin embargo, autores como Montgomery (2020) critican su uso por el riesgo de ser mediciones contaminadas por problemas de control, en cuyo caso el concepto de capacidad carecería de sentido como medida de lo que se puede esperar del proceso en el futuro.
estarían representando la capacidad global del proceso. Sin embargo, autores como Montgomery (2020) critican su uso por el riesgo de ser mediciones contaminadas por problemas de control, en cuyo caso el concepto de capacidad carecería de sentido como medida de lo que se puede esperar del proceso en el futuro.
Recomendaciones prácticas
Para efectos prácticos, sigue la siguientes recomendaciones:
- Usa el
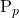 y el
y el 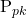 como medidas del rendimiento pasado de tu proceso.
como medidas del rendimiento pasado de tu proceso. - Usa el
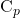 y
y 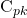 como medidas de la capacidad que puedes esperar de tu proceso en el futuro, tras verificar que tu proceso está en control.
como medidas de la capacidad que puedes esperar de tu proceso en el futuro, tras verificar que tu proceso está en control. - Que el
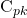 difiera mucho del
difiera mucho del 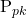 es un indicador de que el proceso no está bajo control. Cuando el proceso no está en control,
es un indicador de que el proceso no está bajo control. Cuando el proceso no está en control, 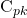 es el rendimiento que podrías lograr, en términos de
es el rendimiento que podrías lograr, en términos de 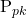 si logras regresar el proceso a estado de control.
si logras regresar el proceso a estado de control.
Ejemplo numérico
Para ilustrar el cálculo de la capacidad de los procesos variables, o con mediciones cuantitativas, veamos el caso de un problema que me atañe mucho a nivel personal, la extracción de café espresso, o expreso en español. El proceso de extracción de café espresso depende de muchas variables como: grado de molienda, edad del café, tipo de café, temperatura del agua, presión del agua, el perfil barométrico, volumen del agua, gramaje del café molido, tiempo de pre-infusión, etc. De esta forma, encontrar la combinación correcta de niveles que generan el mejor sabor del café es todo un reto. Existen muchas recetas para una buena taza de café. Sin embargo, dentro de este caos existe una constante en la que muchos expertos están de acuerdo, una extracción exitosa de café espresso resulta en un tiempo de extracción cercano a los 30 segundos. Este tiempo es medido desde la caída de la primera gota hasta completar 2 onzas de café extraído. En la Tabla 2 encontramos 10 muestras de 6 tiempos de extracción por día extraídas de una máquina de café espresso. Deseamos saber qué tan bien cumple este proceso los requerimientos de mantener tiempos de extracción de 30 segundos, con tolerancias de 25 a 35 segundos.
| día | x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|---|
| 1 | 28.8 | 27.1 | 29.9 | 31.3 | 30.0 | 32.5 |
| 2 | 29.3 | 30.9 | 32.8 | 31.4 | 30.8 | 30.7 |
| 3 | 30.5 | 30.4 | 29.8 | 30.6 | 29.9 | 30.3 |
| 4 | 26.0 | 30.5 | 28.6 | 28.4 | 28.7 | 26.2 |
| 5 | 32.4 | 29.6 | 28.2 | 32.9 | 29.6 | 30.5 |
| 6 | 30.9 | 28.1 | 30.4 | 31.8 | 30.0 | 30.6 |
| 7 | 28.3 | 32.8 | 29.8 | 31.6 | 30.1 | 31.8 |
| 8 | 31.0 | 32.7 | 30.9 | 31.9 | 30.2 | 30.3 |
| 9 | 29.5 | 27.6 | 30.1 | 30.4 | 30.3 | 30.5 |
| 10 | 31.3 | 31.9 | 29.8 | 30.4 | 30.6 | 31.2 |
Para calcular el ![]() y
y ![]() primero debemos constatar que el proceso se encuentre bajo control. Para ello hacemos uso de una carta de control
primero debemos constatar que el proceso se encuentre bajo control. Para ello hacemos uso de una carta de control ![]() , como se observa en la Figura 1.
, como se observa en la Figura 1.
Al observar la Figura 1, notamos que la muestra del día 4 tiene un tiempo promedio inusualmente bajo,en relación a sus los otros subgrupos.
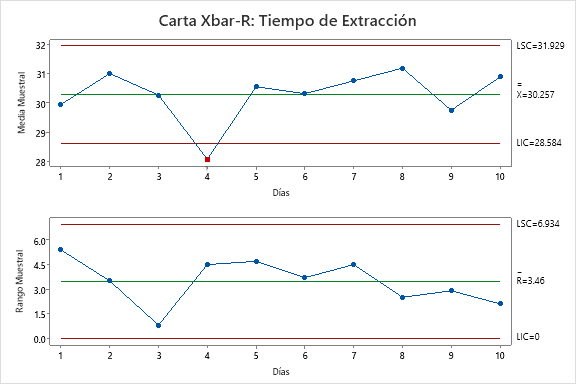
Al indagar con el barista nos dimos cuenta que la muestra del día 4 había sido tomada previo a la calibración del equipo tras la apertura de un nuevo lote de granos de café. Esto implica que la variación registrada en la muestra del día 4 corresponde a una causa asignable de variación, por lo tanto, fuera de control. Evaluamos nuevamente las observaciones, pero ahora omiento de los cálculos las observaciones del día 4. La Figura 2 contiene la nueva gráfica de control ![]() . Aunque aparece evaluado el subgrupo 4, este no fue tomado en cuenta para el cálculo de los límites de control. Observamos que las demás observaciones no muestran evidencia de estar fuera de control.
. Aunque aparece evaluado el subgrupo 4, este no fue tomado en cuenta para el cálculo de los límites de control. Observamos que las demás observaciones no muestran evidencia de estar fuera de control.
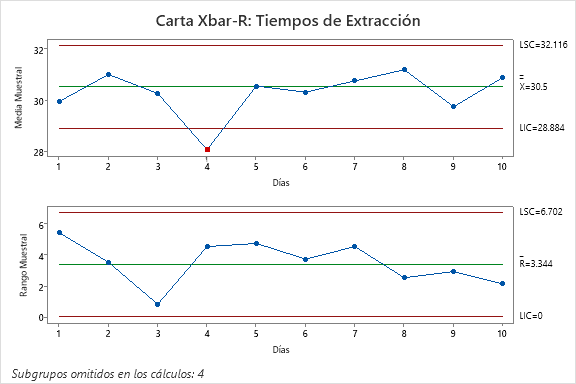
Para terminar de validar si nuestros datos son aptos para ser utilizados para estimar la capacidad de nuestro proceso de extracción de café, procedemos a evaluar la aproximación de los mismos a la normalidad. Para ello realizamos una gráfica cuantil-cuantil, o gráfica de probabilidad, para los tiempo de extracción. El análisis lo realizamos en Minitab, cuyo resultado se muestra en la Figura 3. Aquí se observa que las mediciones se ajustan a la recta esperada para la distribución normal. Además, el valor-p de la prueba de Anderson-Darling es de 0.082, que está por encima del valor de referencia de 0.05, por lo que concluimos que no existe evidencia significativa para suponer falta de normalidad en los datos. Esto no demuestra que nuestros datos sean normales. Recordemos que no podemos probar la hipótesis nula, pero tanto el análisis gráfico como la prueba de Anderson-Darling son consistentes, por lo que consideramos a la distribución normal como un buen modelo a seguir.
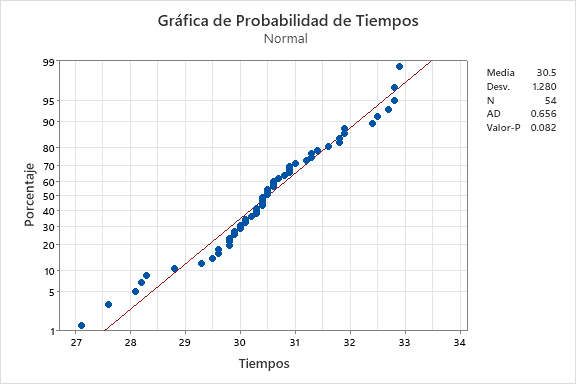
En la Figura 2 podemos observar que ![]() y
y ![]() . Además, de la tabla de constantes, Tabla 1, vemos que
. Además, de la tabla de constantes, Tabla 1, vemos que ![]() . Así,
. Así,
![]()
De esta forma, las métricas de capacidad resultan en,
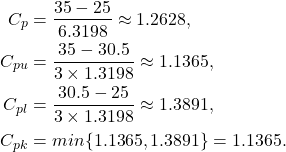
Estos calculos los podemos verificar en Minitab, cuya salida se encuentra en la Figura 4.
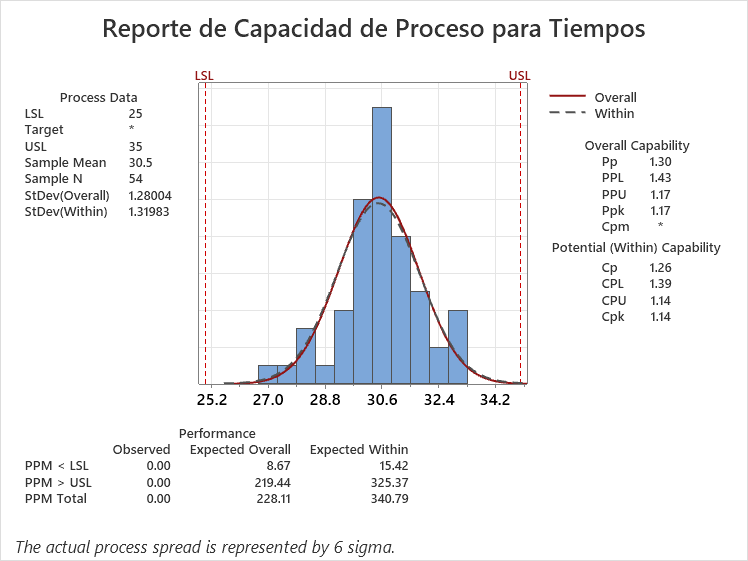
Capacidad de procesos para observaciones de atributos
Cuando observamos atributos, nos limitamos a contar lo que vemos. Contamos piezas no conformes o sus no conformidades, y las registramos en forma de frecuencia, porcentaje, proporción o tasa de aparición. Por ejemplo, contamos el número de botellas no conformes en un lote de 1000, o las burbujas en una ventana laminada.
Como nota para aquellos que recién ingresan al mundo de la ingeniería de calidad. Al evaluar procesos no evaluamos piezas defectuosas, sino piezas no conformes. Tampoco detectamos defectos, sino no conformidades. Aunque a veces los términos se usan como sinónimos. Si nuestras mediciones son buenas, los artículos no conformes coincidirán con los artículos defectuosos, y las no conformidades con los defectos.
Entre las métricas más usadas para evaluar las observaciones por atributo prestamos especial atención a dos: proporciones y tasas. A continuación ilustro su uso como medidas de capacidad.
Proporciones
Cuando lideamos con una situación similar al conteo de artículos no conformes por lote, la proporción de no conformes la calculamos de la siguiente manera:
![]()
Para ilustrar el análisis de capacidad hacemos uso de las muestras registradas en la Tabla 3, donde se observa un registro de no conformidades encontradas en lotes de 200 bolsas de café.
| Lote | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| No conformes | 8 | 6 | 26 | 7 | 13 | 8 | 9 | 9 | 11 | 8 |
Tras evaluar los datos mediante una carta de control P, en la Figura 5, encontramos un problema en la muestra 3. Una revisión en los registros indica que hubo un problema de producción en la impresión de los logos de ese día. Esto implica que el lote 3 corresponde a una causa especial de variación, por lo tanto debe ser eliminado del cálculo del nivel de capacidad.
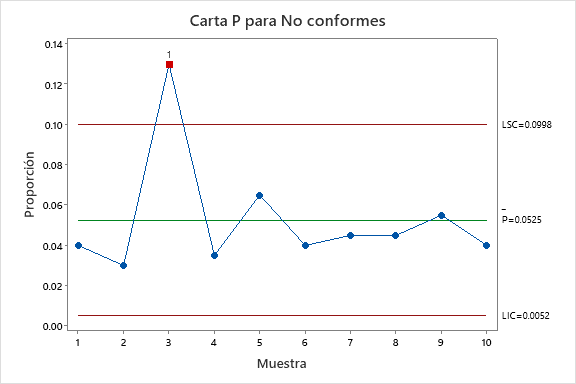
Tras identificar el lote 3 como lote con causa asignable, volvemos a correr la carta de control P, como se ve en la Figura 6, sólo que ahora se omite de los cálculos el lote problemático. El resultado es una capacidad, en términos de proporción, de
![]()
El resultado anterior lo obtenemos de sumar el total de 79 bolsas no conformes, sin incluir el lote 3, entre el total de 1800 bolsas inspeccionadas, también sin incluir el lote 3 por estar validado como fuera de control. Esta capacidad ![]() coincide con los resultados de Minitab en la Figura 6.
coincide con los resultados de Minitab en la Figura 6.
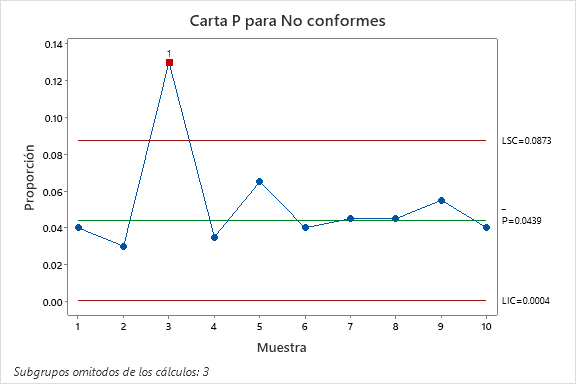
Es necesario observar que habrá situaciones donde al momento de evaluar tus datos mediante una carta de control encuentres señales de alarma donde no hay causas asignables de variación que demuestren una falta real de control. Estas son falsas alarmas, y las falsas alarmas no se excluyen de tus cálculos, sino estarías sesgando tus estimaciones de capacidad. Esta regla aplica tanto para el análisis de capacidad de datos variables como de atributos.
Tasas
Una tasa es una relación entre dos mediciones. Cuando evaluamos procesos, es común no sólo evaluar el número de partes no conformes, sino cuantas no conformidades o defectos ocurrieron. Una métrica utilizada en este sentido es la tasa de no conformidades
![]()
Esta tasa corresponde al número de defectos por unidad, o simplemente DPU. Los defectos por unidad, en manufactura, frecuentemente se modelan utilizando la distribución Poisson. Por lo tanto, para validar que las mediciones que tenemos están bajo control y así poder determinar la capacidad del proceso usaremos una carta de control U. Para ilustrar, utilizamos como ejemplo las mediciones de granos de café mal tostado por kilo de producto inspeccionado mostradas en la Tabla 4.
| Lote | Kilos | No conformidades |
| 1 | 2 | 6 |
| 2 | 2 | 7 |
| 3 | 2 | 2 |
| 4 | 2 | 2 |
| 5 | 2 | 5 |
| 6 | 4 | 15 |
| 7 | 3 | 5 |
| 8 | 2 | 6 |
| 9 | 1 | 2 |
| 10 | 6 | 11 |
Estrictamente hablando, al usar la carta de control U para evaluar los datos, como se muestra en la Figura 7, estamos usando la aproximación de la distribución Poisson ala binomial, una situación válida cuando el número de unidades inspeccionadas (granos de café por kilo) es grande y la cantidad de artículos no conformes (granos no conformes) es pequeña.
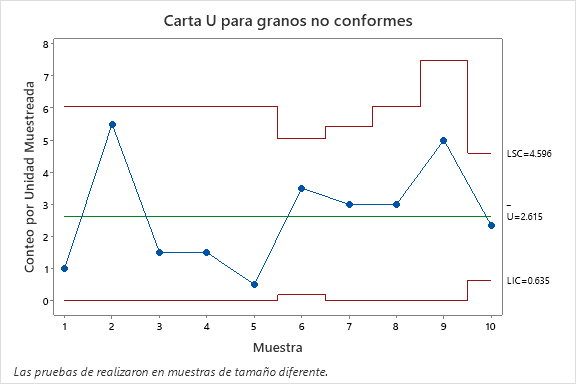
Dado que el proceso se muestra bajo control, procedemos a calcular su capacidad como
![]()
Observamos que el valor de la línea central de la Figura 7 coincide con nuestros cálculos.
Para concluir
En este artículo hemos resaltado uno de los requisitos claves y frecuentemente olvidados al momento de medir la capacidad de nuestros procesos, el estado de control. Si tu proceso no se encuentra en control, tu índice de control no será más que una medición del rendimiento, una vista hacia el pasado. Cuando un proceso está bajo control, el proceso es predecible, dentro de cierto rango, por lo tanto, la medición que hacemos de capacidad permite proyectar el estado del proceso hacia el futuro, siempre que las condiciones de control se mantengan.
Cuando nuestras observaciones siguen una distribución normal, la media y la desviación estándar caracterizan completamente la distribución de las mediciones. Por lo tanto, índices como el ![]() y
y ![]() que comparan estos estadísticos con las tolerancias del cliente tienden a ser suficientes. Por otro lado, si nuestras observaciones son de atributos, la proporción que medimos al registrar productos no conformes caracteriza correctamente la distribución binomial, la correspondiente en esta situación. Así mismo, en caso de medir no conformidades o defectos, la distribución Poisson tiende a ser un buen ajuste, y los DPU o tasa de no conformidades es suficiente representación del proceso.
que comparan estos estadísticos con las tolerancias del cliente tienden a ser suficientes. Por otro lado, si nuestras observaciones son de atributos, la proporción que medimos al registrar productos no conformes caracteriza correctamente la distribución binomial, la correspondiente en esta situación. Así mismo, en caso de medir no conformidades o defectos, la distribución Poisson tiende a ser un buen ajuste, y los DPU o tasa de no conformidades es suficiente representación del proceso.
Para ilustrar el análisis de capacidad tanto para datos variables como de atributo, repasamos los cálculos con ejemplos basados en la elaboración de café espresso, como el utilizado en el latte de la Figura 8 en un desafortunado intento por crear una figura rosetta. Aunque algunas de estas observaciones usadas en los ejemplos son reales, otras fuera obtenidas de un proceso de sintético del mismo proceso, manteniendo siempre el espíritu de la producción real.
En todos los casos discutidos, el estado de control es la clave. No se puede hablar de capacidad sin hablar de control. Recuerda esta máxima en tu próxima reunión de seguimiento y al momento de elaborar tu siguiente reporte de producción.

Referencias
Kane, V. E. (1986). Process capability indices. Journal of quality technology, 18(1), 41-52.
Frank M. Gryna (1999). Operations. Juran’s Quality Handbook (5ta Edición). McGraw-Hill, United States of America. (Joseph M. Juran, co-editor-in-chief, A. Blanton Godfrey, co-editor-in-chief).
Montgomery, D. C. (2020). Introduction to statistical quality control. John Wiley & Sons.
Rodriguez, R. N. (1992). Recent developments in process capability analysis. Journal of Quality Technology, 24(4), 176-187.
Salazar-Alvarez, M. I., Temblador-Pérez, C., Conover, W. J., Tercero-Gómez, V. G., Cordero-Franco, A. E., & Beruvides, M. G. (2016). Regressing sample quantiles to perform nonparametric capability analysis. The International Journal of Advanced Manufacturing Technology, 86(5), 1347-1356.
