En nuestro afán para mejorar la calidad de un sistema, sea de manufactura o servicio, cuando hemos identificado la relación que existe entre los factores críticos controlables del sistema estudiado (X) y las características de calidad que deseamos mejorar (Y), el problema de la mejora se reduce a encontrar un nivel apropiado en los factores para obtener el efecto deseado en las características de calidad. Para esto usamos la relación Y=f(X), conocida en metodologías como Seis Sigma como la función de transferencia, y se considera esencial para guiar la mejora. Esta ecuación representa el conocimiento que tenemos de un proceso y es la llave para definir su curso. Cuando desconocemos la función de transferencia, recurrimos a diversas estrategias de ingeniería, estadística y modelación matemática que nos ayudan a su construcción en dependencia del nivel de desconocimiento que tengamos. Hacernos conscientes del desconocimiento nos ayudar a enfocar nuestro esfuerzo de mejora. Será en dependencia de este desconocimiento que aplicaremos alguna de las 5 claves para la mejora de procesos.
Como recurso mnemotécnico para recordar estas claves, he propuesto usar el nombre HOMER, que posiblemente asocies al escritor de la Odisea o al personaje del mismo nombre en la serie de televisión Los Simpson. Estrategias para mejorar procesos existen muchas, desde el ciclo de Deming hasta los proyectos Lean Seis Sigma hay toda una gama de enfoques y rutinas que nos ayudan a encontrar la solución a nuestros problemas. A diferencia de estas propuestas, HOMER es un enfoque basado en el nivel de desconocimiento, desde una perspectiva de la ingeniería industrial, ingeniería de calidad, matemáticas y estadísticas, y mi experiencia personal de 15 años como instructor, investigador y consultor en proyectos industriales. Así, las 5 claves para la mejora de procesos son:
- Hacer: Si sabes lo que tienes que hacer, ¡hazlo!
- Optimizar: Si desconoces los niveles óptimos, optimiza.
- Modelar: Si desconoces la relación Y=f(X), modela.
- Evaluar: Si desconoces las variables críticas, evalúa tus hipótesis.
- Recolectar: Si desconoces las variables involucradas, recolecta información y déjate sorprender.
Hacer, optimizar, modelar, evaluar y recolectar (HOMER) representan distintos puntos de partida para un ciclo de mejora basado en el desconocimiento identificado. Siguiendo estas pautas, puedes dar un poco de dirección a la discusión de tus problemas a partir de los cuales podrás definir la mejor ruta de análisis , y, tal vez, aumentar tu probabilidad de éxito en la búsqueda de una solución.
A continuación discuto cada una de estas 5 claves para la mejora de procesos, o HOMER por sus iniciales, partiendo de un estado de conocimiento absoluto, donde sólo tienes que hacer lo que ya sabes que tienes que hacer, y finalizo con el desconocimiento total, donde imperará la acción de recolectar información para observar los fenómenos con la suficiente sensibilidad mental para dejarte sorprender, y en ocasiones, romper tus propios paradigmas. Las acciones de optimizar, modelar y evaluar son etapas intermedias que detonan distintas estrategias de análisis matemático y estadístico.
1. Hacer: si sabes lo que tienes que hacer, ¡hazlo!
La primera acción en HOMER es hacer. A veces, en ambientes organizacionales, algo tan trivial como lo que se espera de nosotros no está claro. Depende del equipo o de una persona en particular responsable que ya ha tomado una decisión. En estas situaciones, es importante ser pragmáticos y aceptar que no podemos cambiar lo que ya ha sido decidido. Averigua si los responsables ya tomaron su decisión sobre el problema que estás analizando y céntrate a implementar la solución establecida sin perder tiempo tratando de cambiar lo que no quiere ser cambiado.
Aunque ciertamente también hay momentos donde debemos armarnos de valor y luchar por un cambio real para lograr una mejora en pos de un bien mayor. Si no tienes el poder, ¡empodérate! Identifica quién está a cargo, presenta tu idea, consigue el apoyo que requieres haciéndote de un champion o sponsor de alto nivel para tu proyecto, y resuelve ese liderazgo sin el cual no podrás lograr ese cambio que buscas.
En otros casos, lo más efectivo podrá ser enfocarnos en lo que podemos controlar y trabajar dentro de nuestra esfera de influencia. Al ser prácticos y enfocarnos en mejorar nuestra perspectiva, habilidades y aquello que esté a nuestro alcance, podemos lograr una mejora significativa en nuestro entorno y así en la calidad de los procesos de la organización.
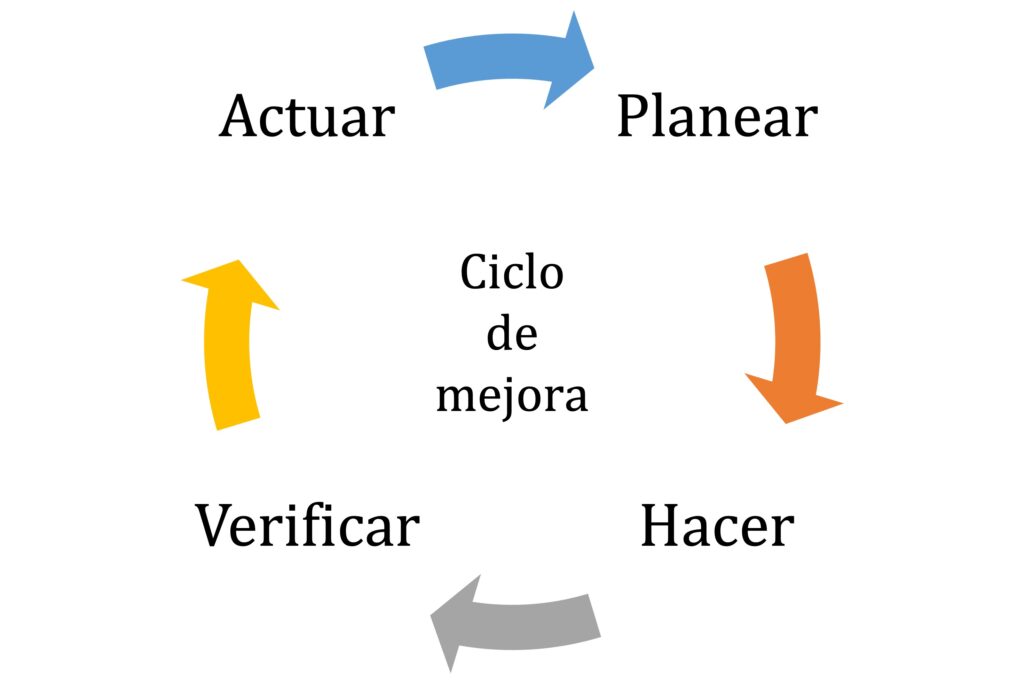
Y no está de más notar que es común encontrarse en situaciones donde se necesita tomar una decisión rápida para solucionar un problema. Sin embargo, buscar la validación necesaria, o sufrir parálisis por análisis, para actuar puede llevar a la procrastinación, a perder tiempo valioso y desesperar. Debemos actuar responsablemente, sin caer en el error de implementar soluciones no exploradas o validadas. Seguir un proceso hacia adelante de verificación y validación nos hará llegar muy lejos. El PDCA de Deming, Figura 1, un método de trabajo sistemático en fases de planear, hacer, verificar y actuar (plan, do, check, act en inglés) viene muy de la mano en estas situaciones cuando deseamos ejecutar una mejora. Si sabemos lo que tenemos que hacer para mejorar la organización, debemos simplemente hacerlo.
2. Optimizar: si desconoces los niveles óptimos, optimiza.
La segunda de las 5 claves para la mejora de procesos, la acción de optimizar en HOMER, es el entendimiento de la relación entre las variables que intervienen en el problema, en particular nuestra función de transferencia Y=f(X). A veces, sin embargo, aunque estas relaciones sean conocidas el problema puede ser significativamente complejo y su solución nada intuitiva. Estas situaciones son comunes en el modelado con sistemas de ecuaciones lineales, problemas combinatorios, sistemas de simulación avanzados y modelos dinámicos de ecuaciones diferenciales.
Algunas situaciones donde puedes llegar a conocer el modelo Y=f(X) y reducir el problema a un problema de optimización son las siguientes:
- Problemas de investigación de operaciones como localización de instalaciones, problemas de ruteo, asignación de tareas, etc., representan casos donde con un poco de esfuerzo se puede modelar el sistema completo de variables y restricciones, y su solución óptima requiere de altos esfuerzos computacionales. En este tipo de sistemas se suele usar modelos de programación lineal entera mixta. Sistemas como Cplex o Gurobi pueden apoyarnos a encontrar soluciones exactas, pero frecuentemente a un costo computacional alto, por lo que frecuentemente se requiere usar procedimientos heurísticos ad hoc. En la Figura 2 se observa un ejemplo de como lucen este tipo de modelos de optimización matemática.
- Los sistemas de simulación pueden llegar a tener un alto grado de complejidad. En muchas ocasiones la representación del sistema es sorprendentemente fiel, como el caso de los llamados gemelos digitales, que pueden imitar el comportamiento de una máquina hasta el nivel de sus engranes. Mejorar un modelo de este nivel mediante optimización no es una tarea trivial. Algoritmos de búsqueda numéricos, entre los que destacan los populares algoritmos evolutivos, con sus detractores, y el muestreo estadístico, tienden a dar buenos resultados en estas situaciones.
- Los modelos de sistemas dinámicos, frecuentemente establecidos mediante relaciones diferenciales, son populares en la modelación de sistemas físicos y administrativos. Su solución puede ser tan elegante como la solución de un sistema de ecuaciones diferenciales, como modelos compartimentales usados en epidemiología, aunque en la práctica se tendrá que requerir a simulaciones «continuas» para su evaluación. VENSIM, STELLA y MATLAB son softwares populares para la simulación de estos sistemas.
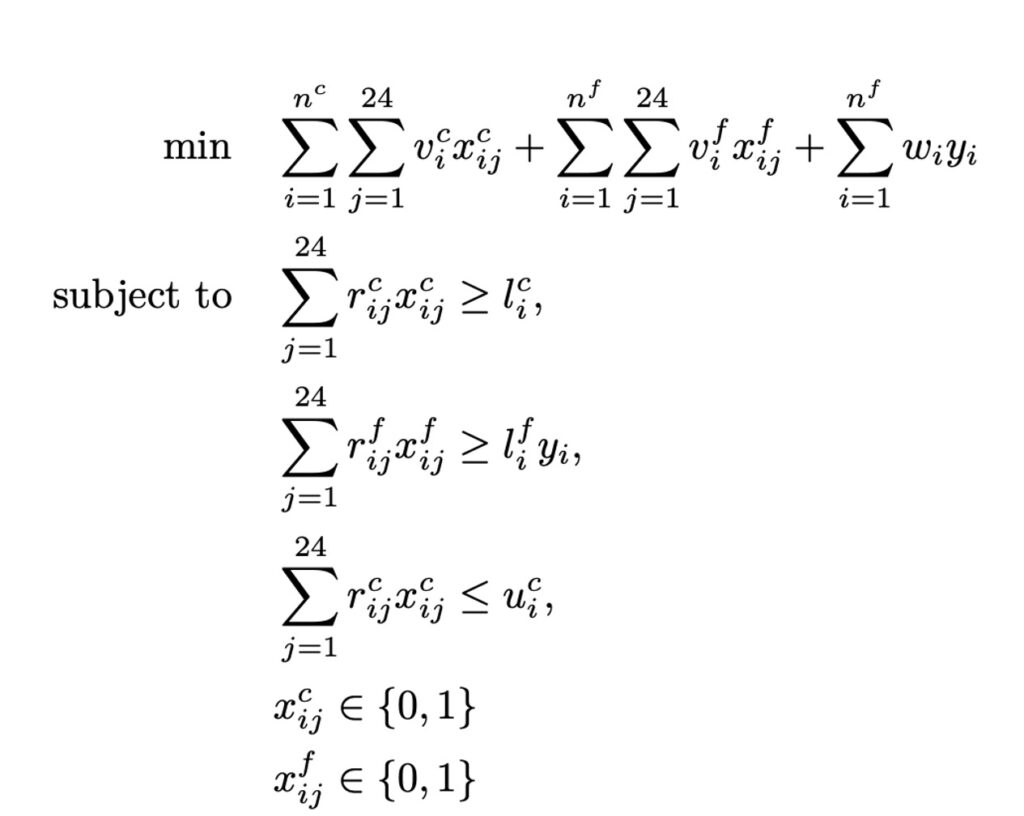
Por supuesto, habrá casos que podrían ser considerados «simples», como lo son algunos modelos aditivos de primer orden, pero no son la norma. En la práctica, son muchos los problemas «difíciles» de solucionar, y pueden requerir de búsquedas entre millares de combinaciones enteras, relaciones no lineales, y con algunas respuestas restringidas a ciertas regiones factibles. En algunos de estos casos el análisis matemático exacto puede ser una ruta para encontrar soluciones, pero su aplicación es limitada a las situaciones con bajo nivel de complejidad. A veces la simplificación que requerimos darle a los problemas para encontrar una solución exacta nos puede alejar tanto de la realidad que terminamos dando soluciones exactas a problemas equivocados.
Una solución menos elegante, pero a la que se le ha encontrado mucha utilidad, es el uso de aproximaciones numéricas mediante el muestreo generado por un diseño de experimentos y el posterior ajuste de funciones empíricas como los modelos de regresión lineal en el análisis de superficies de respuesta. Diseños 2 a la k, fraccionados, cuadrados e hipercuadrados latinos son propuestas muy populares y útiles en esta práctica. Aproximar situaciones exactas con modelos aproximados te puede alejar del óptimo, pero frecuentemente proporcionan soluciones suficientemente buenas para ser prácticas.
Así, la solución de problemas complejos en un proceso de mejora, ya sea por su dimensión y o dificultad computacional, puede ser todo un desafío. Es importante tener la sensibilidad suficiente para reconocer cuándo el problema es de solución simple y cuándo es necesario recurrir a herramientas computacionales o técnicas de optimización más avanzadas, incrementando la complejidad de la solución sólo en la medida en que la solución lo requiera. A veces, las soluciones más prácticas no son las más elegantes, pero aun así son útiles y efectivas en la mejora de los procesos.
3. Modelar: si desconoces la relación Y=f(X), modela.
La tercera de las 5 claves de la mejora de procesos es la modelación. Esta es la acción de modelar en HOMER. Modelamos para simplificar nuestro mundo, nuestro sistema, nuestro problema, y así generar entendimiento. Existen modelos matemáticos, modelos estadísticos, modelos físicos, modelos gráficos, modelos dinámicos, modelos estocásticos, modelos de simulación, modelos conceptuales, y otros muchos que varían según su enfoque y complejidad. En la Figura 3 se muestra un ejemplo de un modelo dinámico. El elemento que tiene todos estos modelos en común es la simplificación de la realidad. No somos capaces de entenderlo todo ni controlarlo todo, por lo que recurrimos a modelos para ajustar los problemas a las limitaciones que como seres humanos tenemos. Aunque, gracias a las tecnologías de la información, muchas de estas limitaciones se han reducido, pero no dejan de existir.
Cuando modelamos, sobre todo al principio de nuestra carrera, es frecuente encontrarnos atrapados en situaciones de nunca acabar. Modelos que nunca satisfacen nuestra necesidad de imitar aquella realidad en la que se inspiran. Siempre falta alguna variable, algún efecto no es exactamente como debería ser, las interacciones están incompletas, el ajuste de las predicciones tiene mucho error, y un largo etcétera de problemas y frustraciones que no tienen fin. Este es el problema de modelar sistemas, procesos y realidades, ¡nunca será suficiente! Por eso, cuando modelamos tenemos que tener claro que el objetivo del modelo no es el de representar fielmente la realidad, basta con ser una aproximación suficientemente buena para tomar aquella decisión que necesitamos tomar. Un buen modelador no modela sistemas, modela problemas.

El modelador experto nunca hablará de crear «el» modelo, sino «un» modelo del problema. El modelador experto sabe que hay muchas formas de representar el mismo problema. Al momento de elegir el enfoque, considera la dificultad del análisis, la interpretabilidad, el uso, y sólo agrega complejidad en la medida en que la necesites. Si el modelo más simple es suficiente para tomar la decisión que requieres tomar, ¡no busques más! Un modelo suficientemente aproximado para solucionar el problema en cuestión es suficiente, y nos damos por bien servidos.
4. Evaluar: si desconoces las variables críticas, evalúa tus hipótesis.
Entramos en una de las zonas más comunes: la acción de evaluar en HOMER. Aquí es cuando no sabemos exactamente qué está afectando a nuestro sistema, pero tenemos algunas sospechas. Necesitamos validarlas. Si tomamos como axiomático que la calidad constante no existe, sólo existe la calidad variable, entonces concluimos, como lo hizo Shewhart en su momento, que el entendimiento de la variabilidad a través de la estadística es el camino a tomar.
Cuando existen sospechas sobre qué variables o factores o causas pueden estar involucradas, un estudio experimental es la mejor opción. No siempre es factible, pero es la mejor opción. Existen dos tipos de estudios: estudios experimentales y estudios observacionales. En el primero tenemos control sobre los factores que deseamos investigar, en el segundo no. Cuando no tenemos el control, al menos intentamos usar información histórica o recolectar datos de los eventos que ocurren y observamos.
El problema de los estudios observacionales es que nos dificultan el obtener conclusiones causa efecto. Cuando no podemos aleatorizar la manera en que evaluamos los tratamientos cuyo efecto queremos estudiar, factores externos en forma de ruido, conocidos o no, pueden generar sesgos en nuestros resultados que ocultarán aquello que deseamos encontrar, o nos harán ver relaciones inexistentes. En este tipo de estudios, debemos usar información a priori sobre el sistema que estamos estudiando y posiblemente incrementar el número de observaciones en la mayor variedad de escenarios para tener algún grado mínimo de confianza al teorizar alguna relación causa efecto más allá de las correlaciones observadas.
Un ejemplo de un estudio observacional lo encontramos al analizar a nuestros clientes. Factores inherentes a los seres humanos, como el género, la edad, la situación social, etc., no pueden ser reasignados entre las personas para un estudio aleatorio,… al menos no sin crear problemas éticos. Estos casos forzosamente tendrán que ser analizados a través de un estudio observacional para clasificar y modelar el comportamiento de nuestros clientes. En los estudios de demanda, el análisis de regresión es probablemente la herramienta más usada para el estudio observacional. En la Figura 4 se observa un ejemplo de regresión lineal simple. El análisis de regresión nos ayuda a modelar lo que observamos, identifica las correlaciones principales entre los factores analizados, y nos ayuda a predecir comportamientos que pueden servir como entrada para el establecimiento de políticas de mercado y diseño de productos.
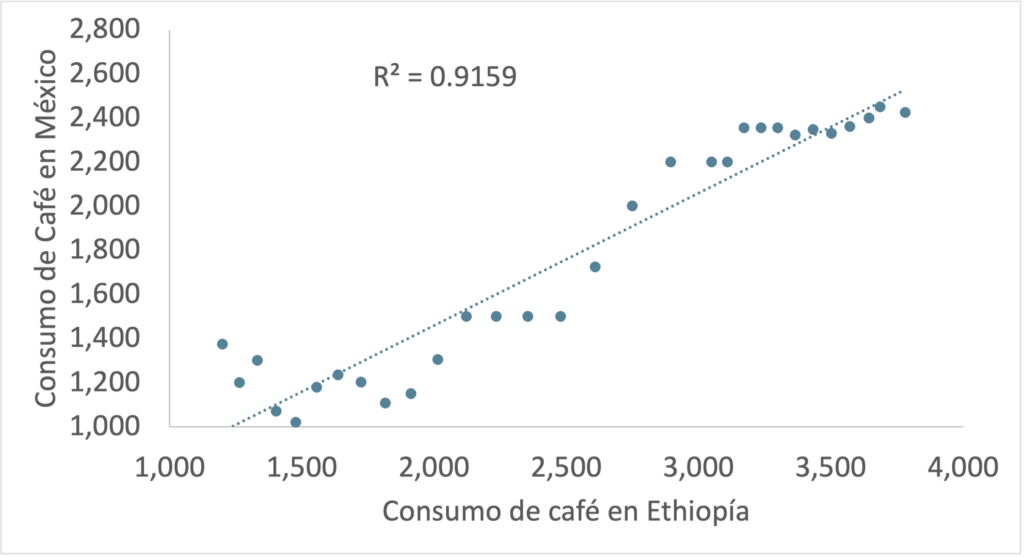
En una situación ideal, los estudios experimentales son la mejor opción. Los estudios experimentales, a través de la aleatorización de los tratamientos analizados, nos permiten distribuir el ruido de factores externos para reducir la probabilidad de sesgos en el análisis, y, con un nivel de confianza controlado, generar conclusiones causa-efecto. Es de recalcar que el objetivo de la aleatorización no es el de reducir el error experimental, sino balancearlo entre los tratamientos estudiados para evitar sesgos. Técnicas como el bloqueo experimental, el uso de co-variables, o el control de factores externos como en un laboratorio efectivamente pueden reducir el ruido experimental, pero es la aleatorización lo que nos dará la seguridad necesaria para validar nuestras hipótesis.
Un ejemplo de un estudio experimental lo encontramos cuando queremos mejorar el rendimiento de un producto. Un proceso de soldadura entre dos piezas puede generar defectos. Estos defectos pueden estar asociados a factores como la inclinación de la varilla de soldadura, el amperaje utilizado y la velocidad de aplicación. Un ingeniero de calidad puede diseñar un experimento donde determinados niveles de estos factores pueden asignarse de forma aleatoria y controlada a las distintas piezas del experimento y así lograr obtener conclusiones causa-efecto sobre los principales responsables de los defectos para su posterior modelación, optimización y mejora.
Si deseas validar hipótesis de forma efectiva, diseña tus experimentos.
5. Recolectar: si desconoces las variables involucradas, recolecta información y déjate sorprender.
La última de las 5 claves de la mejora de procesos es la recolección de información. Aquí, las técnicas usadas en ingeniería para el análisis de causa raíz vienen a ser de mucha ayuda. La acción de recolectar información es la última acción en HOMER. Dimensionar el problema, identificar las variables involucradas y priorizar las más probables son quizá una de las principales razones de la fusión entre la estadística y la ingeniería: la ingeniería estadística.
Para dimensionar el sistema que deseamos analizar e identificar las variables involucradas podemos utilizar diagramas de flujo de procesos y diagramas enriquecidos. Ambos casos serán útiles para identificar los factores involucrados en el problema estudiado.
Los diagramas de flujo de proceso, como el mostrado en la Figura 5, son útiles cuando nos enfrentamos a procesos bien establecidos y repetitivos. Una recomendación al utilizar estos diagramas radica en identificar qué factores son controlables y cuáles no, llegando al detalle de las entradas y salidas de cada actividad, pues al momento de proponer una mejora, serán aquellos factores controlables los que podremos manipular para finalmente establecer una recomendación y mejora.
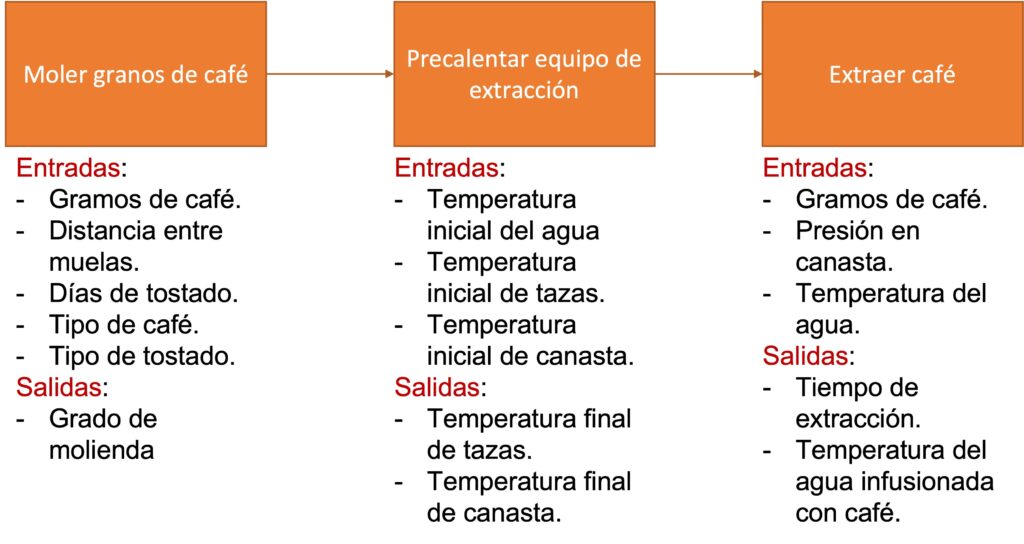
Los diagramas enriquecidos, Figura 6, son también son conocidos como diagramas rich picture. Son útiles para analizar problemas mal definidos y de alta complejidad. La idea de un diagrama enriquecido es la de dibujar el problema en cuestión, con los elementos e interacciones que lo conforman. Si lo puedes dibujar, lo puedes analizar. A diferencia de los diagramas de flujo de procesos, los diagramas enriquecidos permiten incorporar todo tipo de elementos internos o externos al sistema que estudias. Ayudan a encontrar ese consenso de equipo sobre lo que está mal y desean solucionar.
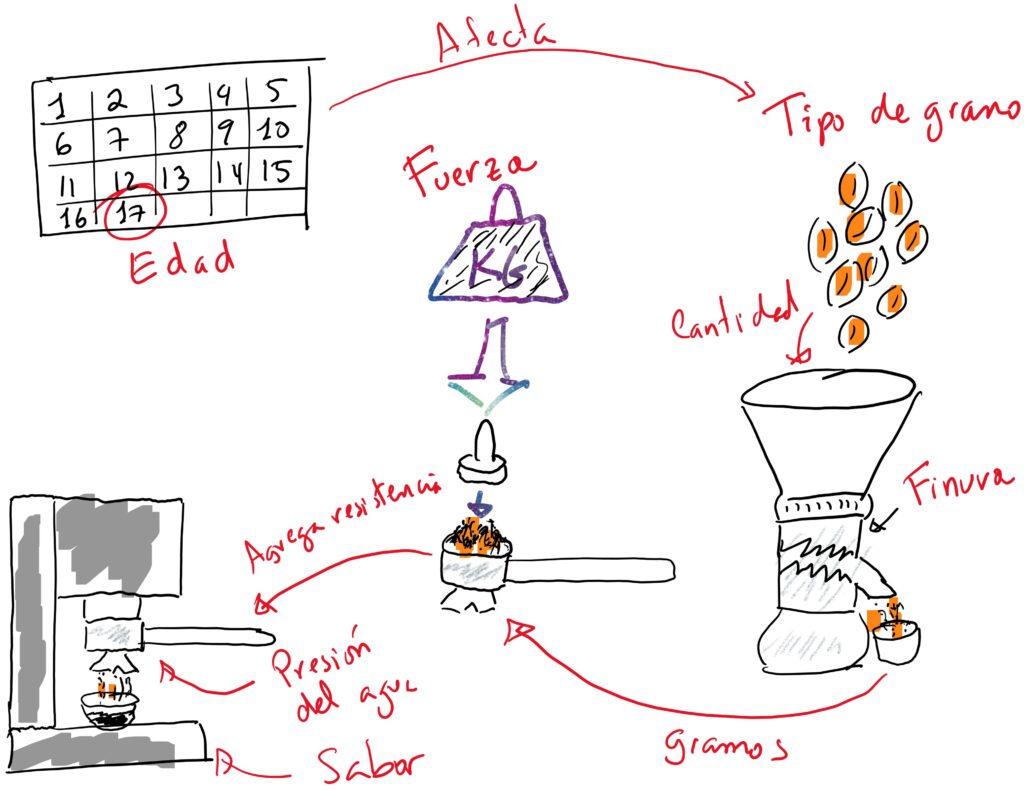
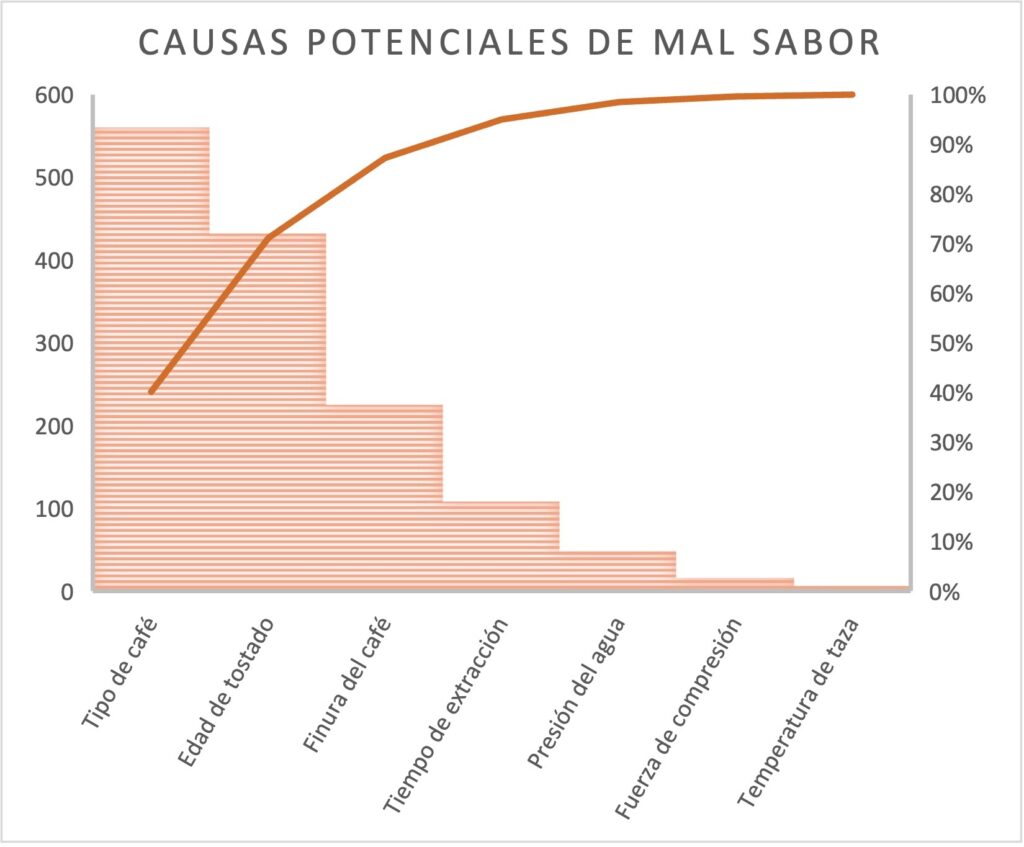
Usar diagramas de flujo de proceso y diagramas enriquecidos puede traer el problema de generar muchas variables potenciales. Herramientas como las matrices causa-efecto y el análisis del modo y efecto de la falla (AMEF) nos ayudan a evaluar y ponderar los posibles factores o variables para encontrar las de mayor potencial. Las ponderaciones establecidas por estas técnicas pueden ser evaluadas por técnicas como la gráfica de Pareto, Figura 7, para establecer aquel 20% de causas críticas que impactan en el 80% de los problemas, y así priorizar.
Cuando la cantidad de variables o factores sea un número manejable, es recomendable crear un plan de recolección de datos para acceder a técnicas exploratorias que nos ayuden a valorar con un poco más de objetividad. El análisis gráfico descriptivo, las tablas de frecuencia, y los resúmenes estadísticos son muy útiles en estas situaciones. Incluso, aún a riesgo de estar cometiendo husmeo de datos, la aplicación de pruebas de hipótesis estadísticas de forma masiva y el uso de niveles de significancia relativamente altos, 0.10 en lugar de 0.05, para rechazar una hipótesis estadística, por ejemplo, son de alta utilidad en estas etapas tempranas de una investigación. Más tarde podrás, y deberás, hacer pruebas de validación con aquellas pocas variables que identifiques como altamente probables de afectar tu problema bajo estudio.
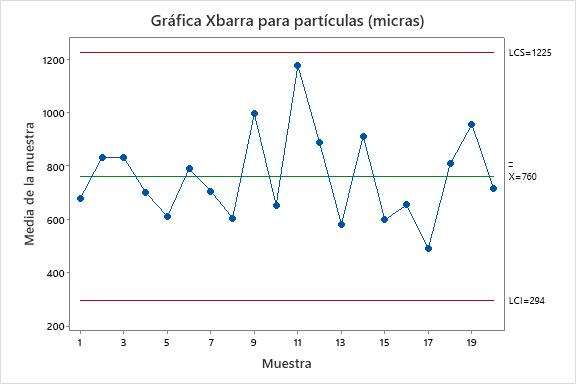
Y cuando no sabes ni por donde iniciar, observa , explora y déjate sorprender. El monitoreo estadístico de procesos (MEP) reúne una serie de métodos utilizados para monitorizar características de calidad en procesos productivos mediante la recolección y el análisis sistemático de los datos. La idea detrás del MEP, con sus cartas de control como la mostrada en la Figura 8, es la de utilizar datos para identificar patrones o tendencias en el rendimiento de los procesos. Cuando monitoreamos procesos mediante una carta de control, eventualmente empezamos a notar cambios en el proceso, sostenidos o aislados, que por medio de investigaciones nos llevan a identificar causas que potencialmente afectan nuestro proceso, y cuyo control y seguimiento representa una fuente invaluable para la mejora.
Conclusiones
Para solucionar problemas, existen muchos enfoques, estrategias, y técnicas que no es posible enumerar y mucho menos discutir apropiadamente en una propuesta condensada como esta. Por ejemplo, técnicas de minería de datos como el análisis de componentes principales, análisis de clusters, identificación de puntos atípicos son especialmente útiles para practicantes avanzados interesados en la exploración que implica la recolección de información y la evaluación de factores. Otras técnicas dentro del aprendizaje de máquina como lo son las redes neuronales artificiales, bosques aleatorios, máquinas de vectores de soporte y otros algoritmos de clasificación pueden ayudar a crear modelos de alta precisión. Más allá de las herramientas específicas listadas o no listadas, es la identificación de la brecha de desconocimiento que te separa de la mejora que buscas lo que marca la pauta para las acciones y herramientas a seleccionar. Una vez identificada la brecha, la combinación de tu experiencia y herramientas adecuadas dentro de las opciones factibles guiará tu análisis.
Estas 5 claves para la mejora de procesos aquí presentadas resumen mis estrategias utilizadas a través de los años ofreciendo consultorías en temas relacionados con la ingeniería de calidad y mejora de procesos. Espero que las iniciales HOMER (hacer, optimizar, modelar, evaluar, recolectar) te ayuden a recordarlas. Son un punto de inicio en el proceso de mejora. En la mayoría de las situaciones he usado enfoques que siguen metodologías como Lean Seis Sigma a través de sus procesos DMAIC, o rutinas de rápida implementación como el ciclo de Deming PDCA, y más recientemente el CRISP-DM en proyectos de ciencia de datos. Con un poco de atención notarás que el método DMAIC de Seis Sigma contempla todas estas acciones en HOMER a lo largo del análisis que propone. La influencia de las matemáticas aplicadas y estadísticas en la resolución de problemas ha estado presente durante todos estos años en estos enfoques. Si tu perfil profesional es analítico, espero hayas encontrado en esta guía algunos tips que te puedan facilitar el camino de resolución de problemas para la mejora de procesos en ingeniería y ciencias.
Si consideras que este enfoque hacia la mejora de procesos te puede ayudar a diagnosticar y organizar tus iniciativas, y mi apoyo te puede ser útil, no dudes en contactarme. Juntos podemos encontrar esa ruta metodológica y técnica hacia el nivel de calidad que necesitas.


Muy buen artículo. Gracias por compartir.